【導(dǎo)讀】在這里，作者將嘗試找出關(guān)于極點(diǎn)和零點(diǎn)的物理感覺(jué)，使用運(yùn)算放大器來(lái)控制它們?cè)趶?fù)平面中的位置，并利用電路的自然響應(yīng)來(lái)說(shuō)明極點(diǎn)/零點(diǎn)位置的影響。
單端口電路的自然響應(yīng)
我們來(lái)看圖1中的無(wú)源線性單端口電路，它包括電阻、電容和電感。
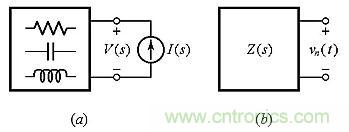
圖1：（a）無(wú)源單端口電路 （b）自然（或無(wú)源）開(kāi)路響應(yīng)vn(t)。
如果我們施加一個(gè)測(cè)試電流I(s)，單端口電路將產(chǎn)生電壓V(s)，使得V(s)=Z(s)/(s)，其中I(s)和V(s)是所施加電流和所產(chǎn)生電壓的拉普拉斯變換，s是以sec-1為單位的復(fù)數(shù)頻率。阻抗Z(s)是s的有理函數(shù)形式，即分子多項(xiàng)式N(s)與分母多項(xiàng)式D(s)的比值：
公式N(s)=0的根被稱為Z(s)的零點(diǎn)，表示為z1，z2，……；而公式D(s)=0的根被稱為Z(s)的極點(diǎn)，表示為p1、p2、……。極點(diǎn)和零點(diǎn)統(tǒng)稱為根，也稱為臨界頻率。例如，阻抗：
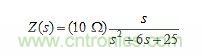
當(dāng)s=0時(shí)，其值為零；當(dāng)s=-3±j4時(shí)，它具有復(fù)共軛極點(diǎn)對(duì)?？梢杂酶鶃?lái)表達(dá)它，即：
如果我們繪制|Z(s)|相對(duì)于s的幅度曲線，則可以直觀理解零點(diǎn)和極點(diǎn)的含義。所得到的曲線就好像在s平面上豎起的帳篷，在零點(diǎn)處接觸s平面，而在極點(diǎn)處其高度變?yōu)闊o(wú)限。
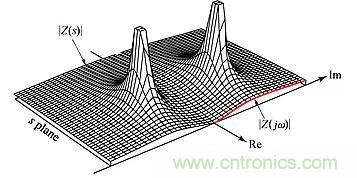
圖2：Z(s)=(10Ω)s/(s2+6s+25)的幅度圖。（通過(guò)在虛軸上計(jì)算|Z|獲得的分布曲線圖顯示出單端口電路的交流響應(yīng)。）
為了找到極點(diǎn)的物理感覺(jué)，我們?cè)趕接近極點(diǎn)pk時(shí)施加電流I(s)，就可以用相當(dāng)小的I(s)獲得給定的電壓V(s)。s越接近極點(diǎn)pk，獲得給定電壓V(s)所需的電流I(s)越小。在s→pk的極限狀態(tài)下，即使電流為零，即開(kāi)路，單端口電路也會(huì)獲得一個(gè)非零的供電電壓（見(jiàn)圖1b）！這個(gè)電壓稱為自然響應(yīng)或無(wú)源響應(yīng)，因?yàn)閱味丝陔娐房衫脙?chǔ)存在其電容和電感內(nèi)部的能量來(lái)產(chǎn)生電壓。這些能量在電阻中消耗盡了，在無(wú)源單端口的情況下，它們將隨時(shí)間呈指數(shù)級(jí)衰減。實(shí)際上，系統(tǒng)理論預(yù)測(cè)到自然響應(yīng)符合以下表達(dá)式：
其中a1，a2，......，是取決于存儲(chǔ)能量的合適系數(shù)（以V為單位），Z(s)的極點(diǎn)是指數(shù)中時(shí)間常數(shù)的倒數(shù)。
那么Z(s)的零點(diǎn)呢？我們來(lái)看圖3，它表示圖1的兩種情況?，F(xiàn)在施加的信號(hào)是電壓V(s)，而響應(yīng)是電流I(s)=[1/Z(s)]V(s)，這表明Z(s)的零點(diǎn)現(xiàn)在成為1/Z(s)的極點(diǎn)。通過(guò)雙重推理，在s→zk的極限狀態(tài)下，即使施加零電壓（短路），單端口電路也將提供非零電流（參見(jiàn)圖3b）！該電流稱為自然響應(yīng)或無(wú)源響應(yīng)，因?yàn)閱味丝陔娐防脙?chǔ)存在其電容和電感內(nèi)部的能量來(lái)產(chǎn)生電流。系統(tǒng)理論預(yù)測(cè)自然短路電流響應(yīng)符合以下表達(dá)式：
其中b1，b2，......，是取決于存儲(chǔ)能量的合適系數(shù)（以安培為單位），Z(s)的零點(diǎn)是指數(shù)中時(shí)間常數(shù)的倒數(shù)。
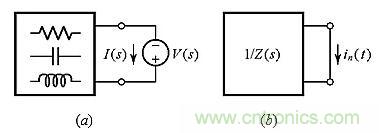
圖3：（a）無(wú)源單端口電路（b）自然（或無(wú)源）短路響應(yīng)in(t)。
總而言之，單端口電路的自然響應(yīng)由其阻抗Z(s)的根控制：極點(diǎn)控制開(kāi)路電壓響應(yīng)vn(t)，而零點(diǎn)控制短路電流響應(yīng)in(t)。在某種程度上，根就像是單端口電路的DNA。例如，我們來(lái)看圖4的單端口電路。在t=0時(shí)，電容兩端的電壓為9V，頂部為正，t>0時(shí)它的自然響應(yīng)是什么？可以看出單端口電路呈現(xiàn)的阻抗是：
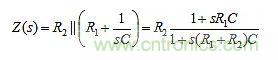
顯然，z1=–1/(R1C)=-1/(10ms)，p1=-1/[(R1+R2)C]=-1/(30ms)。此外，a1=[20/(10+20)]9=6V且b1=9/10=0.9mA。所以：
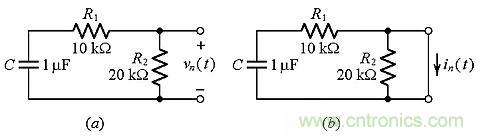
圖4：找出（a）開(kāi)路和（b）短路的自然響應(yīng)。
單極點(diǎn)控制
在圖5a的電路中，由vn表示的節(jié)點(diǎn)和地之間的阻抗為Z(s)=R||(1/sC)=R/(1+sRC)，因此在s=-1/(RC)=-1/(1ms)時(shí)電路具有一個(gè)極點(diǎn)。假設(shè)vn(0)=1V，我們可以得到：
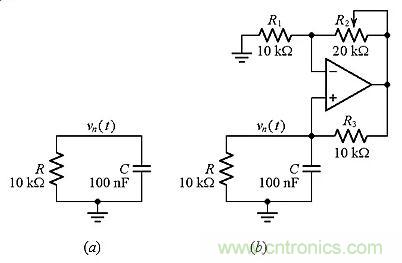
圖5：（a）基本電路（b）相同的電路，但可以控制極點(diǎn)。
無(wú)論怎樣選擇R和C的值，該電路的極點(diǎn)將始終為負(fù)。我們希望找到控制它的方法，以便將其驅(qū)動(dòng)為零甚至使其成為正的。圖5b示出的電路可以完成這項(xiàng)工作。非反相放大器檢測(cè)vn并輸出電壓：
(1 + R2/R1)vn = (1 + k)vn
k = R2/R1
其中R2代表電位器在其左端和游標(biāo)之間的部分。對(duì)于給定的元件值，從左端到右端改變游標(biāo)將使k在0<k<2的范圍內(nèi)變化?，F(xiàn)在，R3上的電壓為(1+k)vn–vn，即kvn，在右邊是正的，表明R3將為C提供電流kvn/R3。鑒于R從C中汲取電流vn/R，因此從C流出的凈電流為iC=vn[1/R+1/(-R3/k)]，表明C視R與一個(gè)負(fù)電阻–R3/k并聯(lián)，凈等效電阻Req=R||(–R3/k)]。擴(kuò)展后可以得到：
對(duì)于給定的元件值，我們有Req=(10kΩ)/(1–k)，因此極點(diǎn)位置現(xiàn)在為s=-1/(ReqC)=-(1–k)/(1ms)，公式（4）變?yōu)椋?/div>
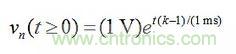
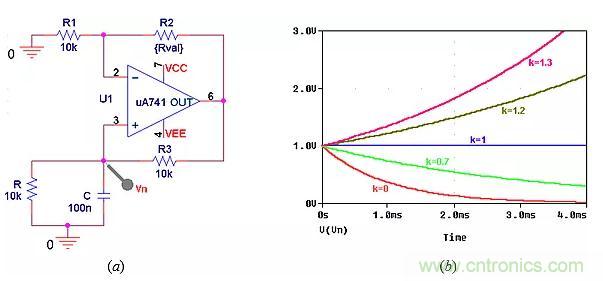
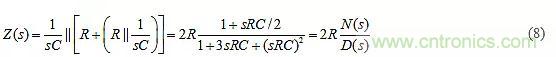
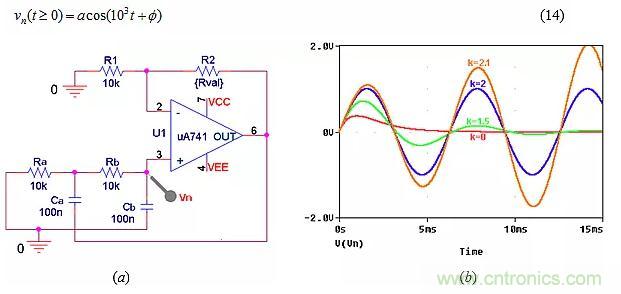
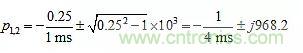
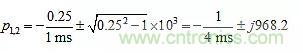
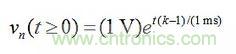
我們討論一下電路作為游標(biāo)設(shè)置函數(shù)的工作原理，使用圖6中的PSpice電路來(lái)顯示隨后的自然響應(yīng)類型。
當(dāng)游標(biāo)一直向左（k=0）時(shí)，R3上的電壓降為零，因此R3帶有零電流，C通過(guò)R放電，時(shí)間常數(shù)為1ms，如公式（4）所示；
將游標(biāo)向右移動(dòng)時(shí)，R3將電流提供給C，只要該電流小于R汲取的電流，C仍然會(huì)呈指數(shù)放電，但速度比k=0時(shí)要慢；
當(dāng)游標(biāo)處于中間（k=1）時(shí)，R3輸出的電流等于R汲取的電流，電容的凈電流為零，因此電容電壓保持恒定；
將游標(biāo)進(jìn)一步向右移動(dòng)（k>1），使得源電流大于汲取電流，因此C呈指數(shù)充電，從而產(chǎn)生不同的響應(yīng)，直到運(yùn)放飽和。
圖6：PSpice電路顯示不同k值的自然響應(yīng)，假設(shè)電容最初充電電壓為1V。
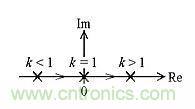
圖7描繪了隨k變化的極點(diǎn)位置。
圖7：極點(diǎn)軌跡是k的函數(shù)。
極點(diǎn)對(duì)控制
在圖8a的電路中，干擾產(chǎn)生自然響應(yīng)vn(t)的阻抗是:
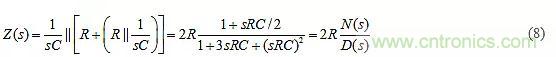
D(s)的階數(shù)表明我們現(xiàn)在有一個(gè)二階系統(tǒng)。對(duì)于這樣的系統(tǒng)，D(s)通常以更方便的形式表達(dá):
其中ζ稱為阻尼比，ω0稱為無(wú)阻尼固有頻率。設(shè)D(s)=0，可以得到極點(diǎn)對(duì)：
比較公式（8）和（9），我們發(fā)現(xiàn)圖8a的電路具有：ζ=1.5和ω0=1/(RC)=1/(1ms)。代入公式（10）得到極點(diǎn)對(duì)p1=-1/(0.3818ms)，p2=-1/(2.618ms)，表示vn(t)由一對(duì)指數(shù)衰減組成，因?yàn)殡娮柘牧舜鎯?chǔ)在電容中的電能。
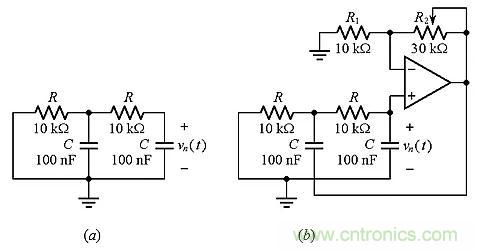
為簡(jiǎn)單起見(jiàn)，假設(shè)圖8a的RC對(duì)完全相同。可以看出，無(wú)論我們?cè)鯓舆x擇元件值，該電路的極點(diǎn)將始終為負(fù)實(shí)數(shù)。
圖8：（a）基本電路（b）相同的電路，但可以控制極點(diǎn)。
我們希望可以找到方法來(lái)控制它們?cè)趶?fù)平面上的位置，以便將它們放置在虛軸上，甚至使它們溢出到復(fù)平面的右半部分。圖8b示出了可完成這項(xiàng)工作的電路。其中最左邊的電容被提升離地，由一個(gè)非反相放大器驅(qū)動(dòng)，該放大器檢測(cè)到vn并輸出電壓(1+R2/R1)vn=(1+k)vn，k如公式（5）所示。對(duì)于給定的元件值，從左端到右端改變游標(biāo)將使k在0<k<3的范圍內(nèi)變化。這樣做的目的是想通過(guò)改變k值，使運(yùn)算放大器通過(guò)最左邊電容注入的能量改變甚至超過(guò)電阻消耗的電能。
使用熟悉的電路分析技巧，我們發(fā)現(xiàn)干擾產(chǎn)生自然響應(yīng)vn(t)的阻抗為：
表明2-k=2ζ，或：
ω0=1/(RC)=1/(1ms)。我們來(lái)討論電路隨游標(biāo)設(shè)置變化的工作原理，同樣，使用圖9a的PSpice電路來(lái)顯示隨后的自然響應(yīng)類型，如圖9b所示。
隨著游標(biāo)一直向左滑動(dòng)（k=0），可以得到ζ=1。公式（10）得到重合的極點(diǎn)對(duì)p1=p2=-1/(1ms)。在這種情況下，系統(tǒng)理論預(yù)測(cè)該類型的自然響應(yīng)為：
其中a和b是適合的系數(shù)，取決于t=0時(shí)存儲(chǔ)在電容中的能量。如圖9b所示，在初始浪涌之后，自然響應(yīng)呈指數(shù)衰減至趨于零。
設(shè)k=2，得到ζ=0，所以公式（10）預(yù)測(cè)純虛極點(diǎn)對(duì)p1,2=±j103，其中j是虛數(shù)單位(j2=-1)。使用歐拉公式exp(jα)+exp(–jα)=2cosα，可以看出自然響應(yīng)現(xiàn)在采用這種形式：
圖9：PSpice電路顯示對(duì)應(yīng)于不同k值的自然響應(yīng)，假設(shè)在t=0時(shí)，Ca充電到1V，Cb放電。
其中a和φ是適合的系數(shù)，取決于t=0時(shí)存儲(chǔ)在電容中的能量。其結(jié)果是持續(xù)振蕩，也稱為無(wú)阻尼振蕩（因此稱為ω0）。物理上，運(yùn)算放大器注入單端口電路的能量等于端口電阻消耗的能量，這讓電容以某種乒乓方式交換能量。
● 對(duì)于0<k<2，有1>ζ>0，所以現(xiàn)在公式（10）可以預(yù)測(cè)一對(duì)復(fù)共軛極點(diǎn)。例如，當(dāng)k=1.5時(shí)，由公式（12）得到ζ=0.25，因此由公式（10）得到：
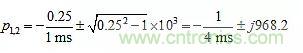
代入公式（2），合并，并再次使用歐拉公式，將得到自然響應(yīng)公式：
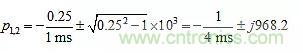
其中a和φ是適合的系數(shù)，取決于t=0時(shí)存儲(chǔ)在電容中的能量。
如圖9b所示，對(duì)于k=1.5，電容仍然以乒乓方式開(kāi)始交換能量，但是該能量逐漸被電阻消耗，從而產(chǎn)生阻尼振蕩。
● 將k提高到2以上，使運(yùn)算放大器注入的能量超過(guò)端口電阻可以消耗的能量，引起發(fā)散振蕩，如圖9b中k=2.1所示。振蕩將持續(xù)增長(zhǎng)到運(yùn)算放大器飽和為止。
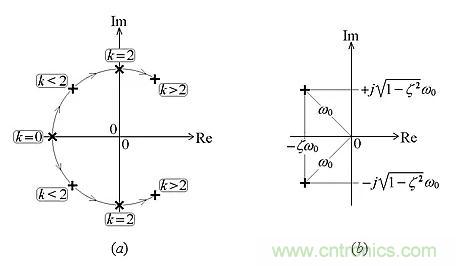
圖10示出了隨k變化的根軌跡?？偠灾?，無(wú)源電路的極點(diǎn)位于復(fù)平面的左半部分。為了使它們溢出到右半平面，我們需要一個(gè)有源元件，例如示例中的運(yùn)算放大器，從自己的電源端獲取能量并將其注入單端口電路。右半平面的極點(diǎn)導(dǎo)致發(fā)散的響應(yīng)，最終使放大器飽和。
圖10：（a）作為k的函數(shù)的根軌跡（b）在阻尼響應(yīng)狀態(tài)下的極點(diǎn)對(duì)。
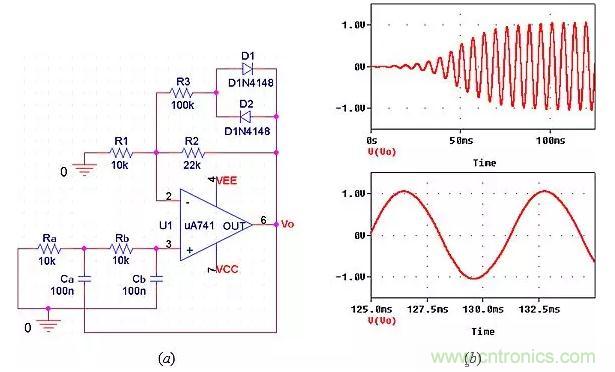
一個(gè)流行應(yīng)用
我們的電路控制極點(diǎn)對(duì)位置的能力可用于產(chǎn)生持續(xù)的正弦波。為此，它需要滿足兩個(gè)條件。
● 為了可以自己?jiǎn)?dòng)，電路的初始配置必須使其極點(diǎn)對(duì)位于復(fù)平面的右半部分（k>2.0）。
圖11：在虛軸上放置并保持一對(duì)極點(diǎn)，以產(chǎn)生正弦波。
即使兩個(gè)電容最初都放電，運(yùn)算放大器的一點(diǎn)噪聲輸入就足以觸發(fā)不斷增長(zhǎng)的振蕩。
● 一旦振蕩達(dá)到所需幅度，就必須采取一些機(jī)制進(jìn)行干預(yù)，以防止其進(jìn)一步增長(zhǎng)，并將其保持在該幅度。這需要將極點(diǎn)對(duì)放置在虛軸（k=2.0）上，并自動(dòng)保持極點(diǎn)在其上，不管元件老化和漂移，或者任何其它干擾。
在圖11a中，電源接通時(shí)，兩個(gè)二極管仍然關(guān)閉，因此k=R2/R1=22/10=2.2，表明振蕩增加。隨著振蕩的增加，二極管在交替的半周期內(nèi)逐漸導(dǎo)通，所以k=[R2||(R3+rd)]/R1，其中rd是動(dòng)態(tài)二極管電阻（rd隨二極管電流而減小）。在rd<<R3的極限情況下，我們將得到k=(22||100)/10=1.8，表示電路可在1.8<k<2.2的范圍內(nèi)調(diào)整k的值，這包括k=2.0時(shí)持續(xù)振蕩達(dá)到所需幅度的情況。
假如由于某種原因?qū)嶋H幅度超過(guò)期望值，rd將減小并導(dǎo)致k降至2.0以下，從而抵消幅度上升。相反，如果幅度降至所需值以下，rd將增加并使k上升到2.0以上，從而抵消幅度下降?？傊挥衚=2.0時(shí)電路才能找到它的“和平”狀態(tài)。“啊，這就是負(fù)反饋的魔力！”作者的一名學(xué)生這樣感慨，他畢業(yè)后去了盧卡斯電影公司工作。
