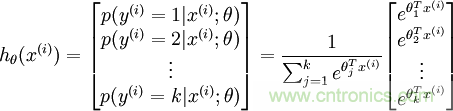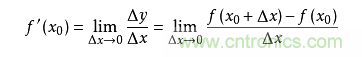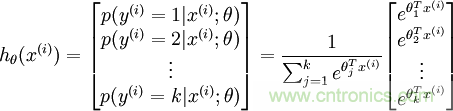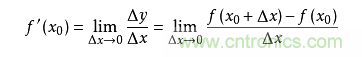【導(dǎo)讀】在深度學(xué)習(xí)出現(xiàn)后，人臉識(shí)別技術(shù)才真正有了可用性。這是因?yàn)橹暗臋C(jī)器學(xué)習(xí)技術(shù)中，難以從圖片中取出合適的特征值。輪廓？顏色？眼睛？如此多的面孔，且隨著年紀(jì)、光線、拍攝角度、氣色、表情、化妝、佩飾掛件等等的不同，同一個(gè)人的面孔照片在照片象素層面上差別很大，憑借專家們的經(jīng)驗(yàn)與試錯(cuò)難以取出準(zhǔn)確率較高的特征值，自然也沒(méi)法對(duì)這些特征值進(jìn)一步分類。
深度學(xué)習(xí)的最大優(yōu)勢(shì)在于由訓(xùn)練算法自行調(diào)整參數(shù)權(quán)重，構(gòu)造出一個(gè)準(zhǔn)確率較高的f(x)函數(shù)，給定一張照片則可以獲取到特征值，進(jìn)而再歸類。
本文中筆者試圖用通俗的語(yǔ)言探討人臉識(shí)別技術(shù)，首先概述人臉識(shí)別技術(shù)，接著探討深度學(xué)習(xí)有效的原因以及梯度下降為什么可以訓(xùn)練出合適的權(quán)重參數(shù)，最后描述基于CNN卷積神經(jīng)網(wǎng)絡(luò)的人臉識(shí)別。
一、人臉識(shí)別技術(shù)概述
人臉識(shí)別技術(shù)大致由人臉檢測(cè)和人臉識(shí)別兩個(gè)環(huán)節(jié)組成。
之所以要有人臉檢測(cè)，不光是為了檢測(cè)出照片上是否有人臉，更重要的是把照片中人臉無(wú)關(guān)的部分刪掉，否則整張照片的像素都傳給f(x)識(shí)別函數(shù)肯定就不可用了。人臉檢測(cè)不一定會(huì)使用深度學(xué)習(xí)技術(shù)，因?yàn)檫@里的技術(shù)要求相對(duì)低一些，只需要知道有沒(méi)有人臉以及人臉在照片中的大致位置即可。一般我們考慮使用OpenCV、dlib等開源庫(kù)的人臉檢測(cè)功能（基于專家經(jīng)驗(yàn)的傳統(tǒng)特征值方法計(jì)算量少?gòu)亩俣雀欤?，也可以使用基于深度學(xué)習(xí)實(shí)現(xiàn)的技術(shù)如MTCNN（在神經(jīng)網(wǎng)絡(luò)較深較寬時(shí)運(yùn)算量大從而慢一些）。
在人臉檢測(cè)環(huán)節(jié)中，我們主要關(guān)注檢測(cè)率、漏檢率、誤檢率三個(gè)指標(biāo)，其中：
• 檢測(cè)率：存在人臉并且被檢測(cè)出的圖像在所有存在人臉圖像中的比例；
• 漏檢率：存在人臉但是沒(méi)有檢測(cè)出的圖像在所有存在人臉圖像中的比例；
• 誤檢率：不存在人臉但是檢測(cè)出存在人臉的圖像在所有不存在人臉圖像中的比例。
當(dāng)然，檢測(cè)速度也很重要。本文不對(duì)人臉檢測(cè)做進(jìn)一步描述。
在人臉識(shí)別環(huán)節(jié)，其應(yīng)用場(chǎng)景一般分為1:1和1:N。
1：1就是判斷兩張照片是否為同一個(gè)人，通常應(yīng)用在人證匹配上，例如身份證與實(shí)時(shí)抓拍照是否為同一個(gè)人，常見(jiàn)于各種營(yíng)業(yè)廳以及后面介紹的1:N場(chǎng)景中的注冊(cè)環(huán)節(jié)。而1:N應(yīng)用場(chǎng)景，則是首先執(zhí)行注冊(cè)環(huán)節(jié)，給定N個(gè)輸入包括人臉照片以及其ID標(biāo)識(shí)，再執(zhí)行識(shí)別環(huán)節(jié)，給定人臉照片作為輸入，輸出則是注冊(cè)環(huán)節(jié)中的某個(gè)ID標(biāo)識(shí)或者不在注冊(cè)照片中?？梢?jiàn)，從概率角度上來(lái)看，前者相對(duì)簡(jiǎn)單許多，且由于證件照通常與當(dāng)下照片年代間隔時(shí)間不定，所以通常我們?cè)O(shè)定的相似度閾值都是比較低的，以此獲得比較好的通過(guò)率，容忍稍高的誤識(shí)別率。
而后者1：N，隨著N的變大，誤識(shí)別率會(huì)升高，識(shí)別時(shí)間也會(huì)增長(zhǎng)，所以相似度閾值通常都設(shè)定得較高，通過(guò)率會(huì)下降。這里簡(jiǎn)單解釋下上面的幾個(gè)名詞：誤識(shí)別率就是照片其實(shí)是A的卻識(shí)別為B的比率；通過(guò)率就是照片確實(shí)是A的，但可能每5張A的照片才能識(shí)別出4張是A其通過(guò)率就為80%；相似度閾值是因?yàn)閷?duì)特征值進(jìn)行分類是概率行為，除非輸入的兩張照片其實(shí)是同一個(gè)文件，否則任何兩張照片之間都有一個(gè)相似度，設(shè)定好相似度閾值后唯有兩張照片的相似度超過(guò)閾值，才認(rèn)為是同一個(gè)人。所以，單純的評(píng)價(jià)某個(gè)人臉識(shí)別算法的準(zhǔn)確率沒(méi)有意義，我們最需要弄清楚的是誤識(shí)別率小于某個(gè)值時(shí)（例如0.1%）的通過(guò)率。不管1:1還是1:N，其底層技術(shù)是相同的，只是難度不同而已。
取出人臉特征值是最難的，那么深度學(xué)習(xí)是如何取特征值的？
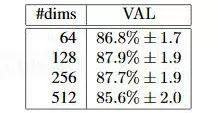
假定我們給出的人臉照片是100*100像素大小，由于每個(gè)像素有RGB三個(gè)通道，每個(gè)像素通道由0-255范圍的字節(jié)表示，則共有3個(gè)100*100的矩陣計(jì)3萬(wàn)個(gè)字節(jié)作為輸入數(shù)據(jù)。深度學(xué)習(xí)實(shí)際上就是生成一個(gè)近似函數(shù)，把上面的輸入值轉(zhuǎn)化為可以用作特征分類的特征值。那么，特征值可以是一個(gè)數(shù)字嗎？當(dāng)然不行，一個(gè)數(shù)字（或者叫標(biāo)量）是無(wú)法有效表示出特征的。通常我們用多個(gè)數(shù)值組成的向量表示特征值，向量的維度即其中的數(shù)值個(gè)數(shù)。特征向量的維度并非越大越好，Google的FaceNet項(xiàng)目（參見(jiàn)https://arxiv.org/abs/1503.03832論文）做過(guò)的測(cè)試結(jié)果顯示，128個(gè)數(shù)值組成的特征向量結(jié)果最好，如下圖所示：
那么，現(xiàn)在問(wèn)題就轉(zhuǎn)化為怎么把3*100*100的矩陣轉(zhuǎn)化為128維的向量，且這個(gè)向量能夠準(zhǔn)確的區(qū)分出不同的人臉？
假定照片為x，特征值為y，也就是說(shuō)存在一個(gè)函數(shù)f(x)=y可以完美的找出照片的人臉特征值?，F(xiàn)在我們有一個(gè)f*(x)近似函數(shù)，其中它有參數(shù)w（或者叫權(quán)重w）可以設(shè)置，例如寫成f*(x;w)，若有訓(xùn)練集x及其id標(biāo)識(shí)y，設(shè)初始參數(shù)p1后，那么每次f*(x;w)得到的y`與實(shí)際標(biāo)識(shí)y相比，若正確則通過(guò)，若錯(cuò)誤則適當(dāng)調(diào)整參數(shù)w，如果能夠正確的調(diào)整好參數(shù)w，f*(x;w)就會(huì)與理想中的f(x)函數(shù)足夠接近，我們就獲得了概率上足夠高準(zhǔn)確率的f*(x;w)函數(shù)。這一過(guò)程叫做監(jiān)督學(xué)習(xí)下的訓(xùn)練。而計(jì)算f*(x;w)值的過(guò)程因?yàn)槭钦５暮瘮?shù)運(yùn)算，我們稱為前向運(yùn)算，而訓(xùn)練過(guò)程中比較y`與實(shí)際標(biāo)識(shí)id值y結(jié)果后，調(diào)整參數(shù)p的過(guò)程則是反過(guò)來(lái)的，稱為反向傳播。
由于我們傳遞的x入?yún)吘故且粡堈掌?，照片既有?duì)焦、光線、角度等導(dǎo)致的不太容易衡量的質(zhì)量問(wèn)題，也有本身的像素?cái)?shù)多少問(wèn)題。如果x本身含有的數(shù)據(jù)太少，即圖片非常不清晰，例如28*28像素的照片，那么誰(shuí)也無(wú)法準(zhǔn)確的分辨出是哪個(gè)人?？梢韵胍?jiàn)，必然像素?cái)?shù)越多識(shí)別也越準(zhǔn)，但像素?cái)?shù)越多導(dǎo)致的計(jì)算、傳輸、存儲(chǔ)消耗也越大，我們需要有根據(jù)地找到合適的閾值。下圖是FaceNet論文的結(jié)果，雖然只是一家之言，但Google的嚴(yán)謹(jǐn)態(tài)度使得數(shù)據(jù)也很有參考價(jià)值。
從圖中可見(jiàn),排除照片其他質(zhì)量外,像素?cái)?shù)至少也要有100*100（純?nèi)四槻糠郑┎拍鼙ＷC比較高的識(shí)別率。
二、深度學(xué)習(xí)技術(shù)的原理
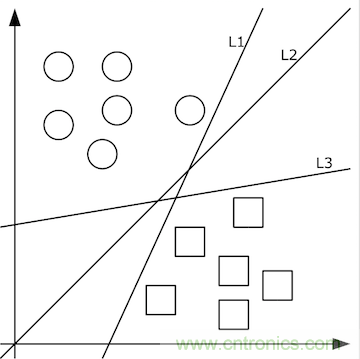
由清晰的人臉照轉(zhuǎn)化出的像素值矩陣，應(yīng)當(dāng)設(shè)計(jì)出什么樣的函數(shù)f(x)轉(zhuǎn)化為特征值呢？這個(gè)問(wèn)題的答案依賴于分類問(wèn)題。即，先不談特征值，首先如何把照片集合按人正確地分類？這里就要先談?wù)剻C(jī)器學(xué)習(xí)。機(jī)器學(xué)習(xí)認(rèn)為可以從有限的訓(xùn)練集樣本中把算法很好地泛化。所以，我們先找到有限的訓(xùn)練集，設(shè)計(jì)好初始函數(shù)f(x;w)，并已經(jīng)量化好了訓(xùn)練集中x->y。如果數(shù)據(jù)x是低維的、簡(jiǎn)單的，例如只有二維，那么分類很簡(jiǎn)單，如下圖所示：
上圖中的二維數(shù)據(jù)x只有方形和圓形兩個(gè)類別y，很好分，我們需要學(xué)習(xí)的分類函數(shù)用最簡(jiǎn)單的f(x,y)=ax+by+c就能表示出分類直線。例如f(x,y)大于0時(shí)表示圓形，小于0時(shí)表示方形。
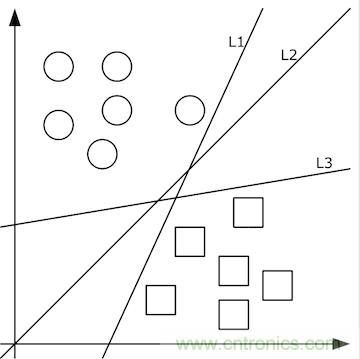
給定隨機(jī)數(shù)作為a,c,b的初始值，我們通過(guò)訓(xùn)練數(shù)據(jù)不斷的優(yōu)化參數(shù)a,b,c，把不合適的L1、L3等分類函數(shù)逐漸訓(xùn)練成L2，這樣的L2去面對(duì)泛化的測(cè)試數(shù)據(jù)就可能獲得更好的效果。然而如果有多個(gè)類別，就需要多條分類直線才能分出，如下圖所示：
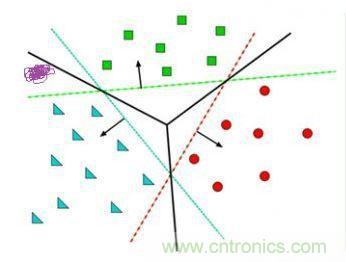
這其實(shí)相當(dāng)于多條分類函數(shù)執(zhí)行與&&、或||操作后的結(jié)果。這個(gè)時(shí)候還可能用f1>0 && f2<0 && f3>0這樣的分類函數(shù)，但如果更復(fù)雜的話，例如本身的特征不明顯也沒(méi)有匯聚在一起，這種找特征的方式就玩不轉(zhuǎn)了，如下圖所示，不同的顏色表示不同的分類，此時(shí)的訓(xùn)練數(shù)據(jù)完全是非線性可分的狀態(tài)：
這個(gè)時(shí)候，我們可以通過(guò)多層函數(shù)嵌套的方法來(lái)解決，例如f(x)=f1(f2(x))，這樣f2函數(shù)可以是數(shù)條直線，而f1函數(shù)可以通過(guò)不同的權(quán)重w以及激勵(lì)函數(shù)完成與&&、或||等等操作。這里只有兩層函數(shù)，如果函數(shù)嵌套層數(shù)越多，它越能表達(dá)出復(fù)雜的分類方法，這對(duì)高維數(shù)據(jù)很有幫助。例如我們的照片毫無(wú)疑問(wèn)就是這樣的輸入。所謂激勵(lì)函數(shù)就是把函數(shù)f計(jì)算出的非常大的值域轉(zhuǎn)化為[0,1]這樣較小的值域，這允許多層函數(shù)不斷地前向運(yùn)算、分類。
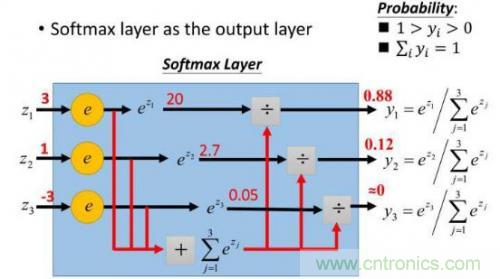
前向運(yùn)算只是把輸入交給f1(x,w1)函數(shù)，計(jì)算出的值再交給f2(y1,w2)函數(shù)，依次類推，很簡(jiǎn)單就可以得到最終的分類值。但是，因?yàn)槌跏嫉膚權(quán)重其實(shí)沒(méi)有多大意義，它得出的分類值f*(x)肯定是錯(cuò)的，在訓(xùn)練集上我們知道正確的值y，那么事實(shí)上我們其實(shí)是希望y-f*(x)的值最小，這樣分類就越準(zhǔn)。這其實(shí)變成了求最小值的問(wèn)題。當(dāng)然，y-f*(x)只是示意，事實(shí)上我們得到的f*(x)只是落到各個(gè)分類上的概率，把這個(gè)概率與真實(shí)的分類相比較得到最小值的過(guò)程，我們稱為損失函數(shù)，其值為loss，我們的目標(biāo)是把損失函數(shù)的值loss最小化。在人臉識(shí)別場(chǎng)景中，softmax是一個(gè)效果比較好的損失函數(shù)，我們簡(jiǎn)單看下它是如何使用的。
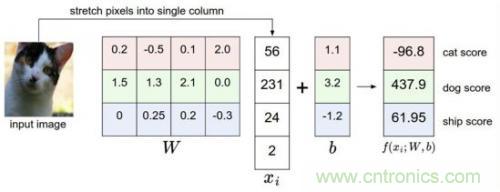
比如我們有訓(xùn)練數(shù)據(jù)集照片對(duì)應(yīng)著cat、dog、ship三個(gè)類別，某個(gè)輸入照片經(jīng)過(guò)函數(shù)f(x)=x*W+b，前向運(yùn)算得到該照片屬于這3個(gè)分類的得分值。此時(shí)，這個(gè)函數(shù)被稱為得分函數(shù)，如下圖所示，假設(shè)左邊關(guān)于貓的input image是一個(gè)4維向量[56,231,24,2]，而W權(quán)重是一個(gè)4*3的矩陣，那么相乘后再加上向量[1.1,3.2,-1.2]可得到在cat、 dog、ship三個(gè)類別上的得分：
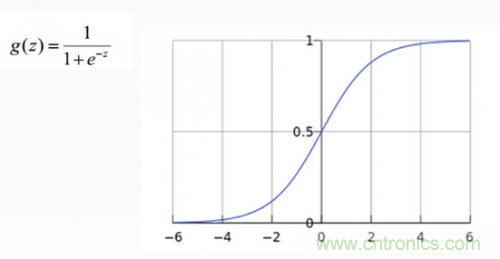
從上圖示例可見(jiàn)，雖然輸入照片是貓，但得分上屬于狗的得分值437.9最高，但究竟比貓和船高多少呢？很難衡量！如果我們把得分值轉(zhuǎn)化為0-100的百分比概率，這就方便度量了。這里我們可以使用sigmoid函數(shù)，如下圖所示：
從上圖公式及圖形可知，sigmoid可以把任意實(shí)數(shù)轉(zhuǎn)換為0-1之間的某個(gè)數(shù)作為概率。但sigmoid概率不具有歸一性，也就是說(shuō)我們需要保證輸入照片在所有類別的概率之和為1，這樣我們還需要對(duì)得分值按softmax方式做以下處理：
這樣給定x后可以得到x在各個(gè)類別下的概率。假定三個(gè)類別的得分值分別為3、1、-3，則按照上面的公式運(yùn)算后可得概率分別為[0.88、0.12、0]，計(jì)算過(guò)程如下圖所示：
然而實(shí)際上x對(duì)應(yīng)的概率其實(shí)是第一類，比如[1,0,0]，現(xiàn)在拿到的概率（或者可稱為似然）是[0.88、0.12、0]。那么它們之間究竟有多大的差距呢？這個(gè)差距就是損失值loss。如何獲取到損失值呢？在softmax里我們用互熵?fù)p失函數(shù)計(jì)算量最?。ǚ奖闱髮?dǎo)），如下所示：
其中i就是正確的分類，例如上面的例子中其loss值就是-ln0.88。這樣我們有了損失函數(shù)f(x)后，怎么調(diào)整x才能夠使得函數(shù)的loss值最小呢？這涉及到微分導(dǎo)數(shù)。
三、梯度下降（上）
梯度下降就是為了快速的調(diào)整權(quán)重w，使得損失函數(shù)f(x;w)的值最小。因?yàn)閾p失函數(shù)的值loss最小，就表示上面所說(shuō)的在訓(xùn)練集上的得分結(jié)果與正確的分類值最接近！
導(dǎo)數(shù)求的是函數(shù)在某一點(diǎn)上的變化率。例如從A點(diǎn)開車到B點(diǎn)，通過(guò)距離和時(shí)間可以算出平均速度，但在其中C點(diǎn)的瞬時(shí)速度是多少呢？如果用x表示時(shí)間，f(x)表示車子從A點(diǎn)駛出的距離，那么在x0的瞬時(shí)速度可以轉(zhuǎn)化為：從x0時(shí)再開一個(gè)很小的時(shí)間，例如1秒，那么這一秒的平均速度就是這一秒開出的距離除以1秒，即(f(1+x0)-f(x0))/1。如果我們用的不是1秒而是1微秒，那么這個(gè)1微秒內(nèi)的平均速度必然更接近x0時(shí)的瞬時(shí)速度。于是，到該時(shí)間段t趨向于0時(shí)，我們就得到了x0時(shí)的瞬時(shí)速度。這個(gè)瞬時(shí)速度就是函數(shù)f在x0上的變化率，所有x上的變化率就構(gòu)成了函數(shù)f(x)的導(dǎo)數(shù)，稱為f`(x)。即：
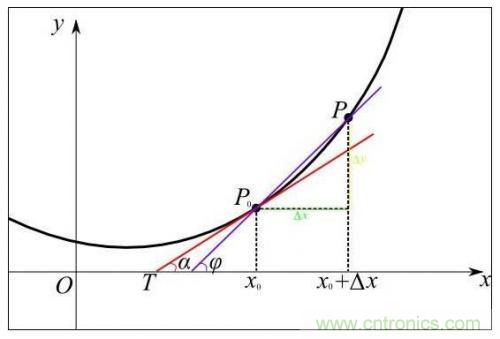
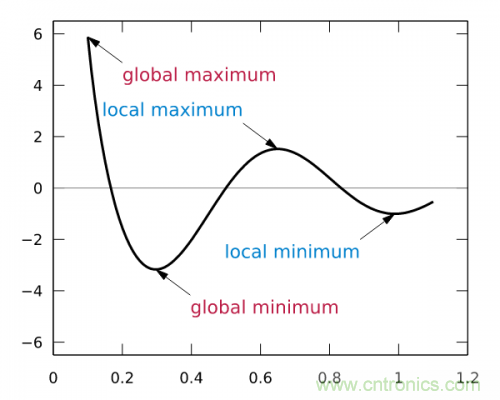
從幾何意義上看，變化率就變成了斜率，這更容易理解怎樣求函數(shù)的最小值。例如下圖中有函數(shù)y=f(x)用粗體黑線表示，其在P0點(diǎn)的變化率就是切線紅線的斜率：
可以形象的看出，當(dāng)斜率的值為正數(shù)時(shí)，把x向左移動(dòng)變小一些，f(x)的值就會(huì)小一些；當(dāng)斜率的值為負(fù)數(shù)時(shí)，把x向右移動(dòng)變大一些，f(x)的值也會(huì)小一些，如下圖所示：
這樣，斜率為0時(shí)我們其實(shí)就得到了函數(shù)f在該點(diǎn)可以得到最小值。那么，把x向左或者向右移一點(diǎn)，到底移多少呢？如果移多了，可能移過(guò)了，如果移得很少，則可能要移很久才能找到最小點(diǎn)。還有一個(gè)問(wèn)題，如果f(x)操作函數(shù)有多個(gè)局部最小點(diǎn)、全局最小點(diǎn)時(shí)，如果x移的非常小，則可能導(dǎo)致通過(guò)導(dǎo)數(shù)只能找到某個(gè)并不足夠小的局部最小點(diǎn)。如下圖所示：
藍(lán)色的為局部最小點(diǎn)，紅色是全局最小點(diǎn)。所以x移動(dòng)多少是個(gè)問(wèn)題，x每次的移動(dòng)步長(zhǎng)過(guò)大或者過(guò)小都可能導(dǎo)致找不到全局最小點(diǎn)。這個(gè)步長(zhǎng)除了跟導(dǎo)數(shù)斜率有關(guān)外，我們還需要有一個(gè)超參數(shù)來(lái)控制它的移動(dòng)速度，這個(gè)超參數(shù)稱為學(xué)習(xí)率，由于它很難優(yōu)化，所以一般需要手動(dòng)設(shè)置而不能自動(dòng)調(diào)整?？紤]到訓(xùn)練時(shí)間也是成本，我們通常在初始訓(xùn)練階段把學(xué)習(xí)率設(shè)的大一些，越往后學(xué)習(xí)率設(shè)的越小。
那么每次移動(dòng)的步長(zhǎng)與導(dǎo)數(shù)的值有關(guān)嗎？這是自然的，導(dǎo)數(shù)的正負(fù)值決定了移動(dòng)的方向，而導(dǎo)數(shù)的絕對(duì)值大小則決定了斜率是否陡峭。越陡峭則移動(dòng)的步長(zhǎng)應(yīng)當(dāng)越大。所以，步長(zhǎng)由學(xué)習(xí)率和導(dǎo)數(shù)共同決定。就像下面這個(gè)函數(shù)，λ是學(xué)習(xí)率，而∂F(ωj) / ∂ωj是在ωj點(diǎn)的導(dǎo)數(shù)。
ωj = ωj – λ ∂F(ωj) / ∂ωj
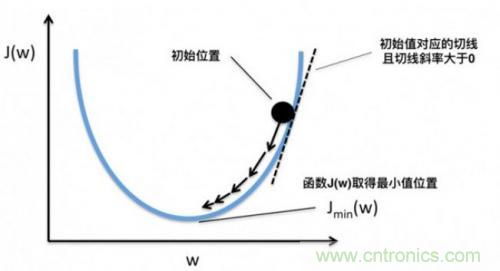
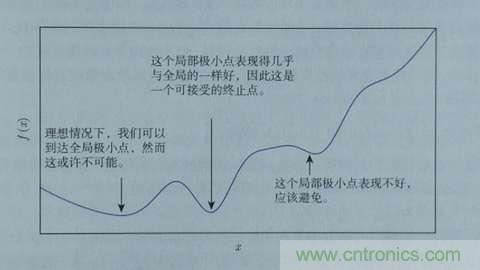
根據(jù)導(dǎo)數(shù)判斷損失函數(shù)f在x0點(diǎn)上應(yīng)當(dāng)如何移動(dòng)，才能使得f最快到達(dá)最小值的方法，我們稱為梯度下降。梯度也就是導(dǎo)數(shù)，沿著負(fù)梯度的方向，按照梯度值控制移動(dòng)步長(zhǎng)，就能快速到達(dá)最小值。當(dāng)然，實(shí)際上我們未必能找到最小點(diǎn)，特別是本身存在多個(gè)最小點(diǎn)時(shí)，但如果這個(gè)值本身也足夠小，我們也是可以接受的，如下圖所示：
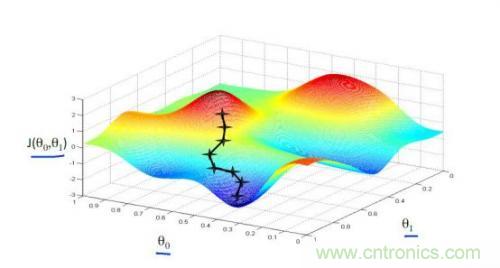
以上我們是以一維數(shù)據(jù)來(lái)看梯度下降，但我們的照片是多維數(shù)據(jù)，此時(shí)如何求導(dǎo)數(shù)？又如何梯度下降呢？此時(shí)我們需要用到偏導(dǎo)數(shù)的概念。其實(shí)它與導(dǎo)數(shù)很相似，因?yàn)閤是多維向量，那么我們假定計(jì)算Xi的導(dǎo)數(shù)時(shí)，x上的其他數(shù)值不變，這就是Xi的偏導(dǎo)數(shù)。此時(shí)應(yīng)用梯度下降法就如下圖所示，θ是二維的，我們分別求θ0和θ1的導(dǎo)數(shù)，就可以同時(shí)從θ0和θ1兩個(gè)方向移動(dòng)相應(yīng)的步長(zhǎng)，尋找最低點(diǎn)，如下圖所示：
